PRA Chinese
Rubber Journal Asia Injection Moulding Asia Energy, Oil & Gas Asia
VISIT OUR OTHER SITES:
PRA Chinese
Rubber Journal Asia
Injection Moulding Asia
Energy, Oil & Gas Asia
Auxiliary Equipment: Investing in a measuring device
Also, download this story from the electronic issue here
This article by Dr. Hilmar Bolte, R&D/ Head of Analysis at German firm Sikora takes a look at the meaning of “measuring rate”, “averaging” and “accuracy” when investing in a measuring device. Founded in 1973, Sikora is a global manufacturer and supplier of measuring and control technology for the wire and cable, hose and tube, sheet and metals as well as optical fibre and plastics industry.
Choosing the optimal measuring device for an extrusion line
When deciding about investing in a measuring device, one of the main factors – besides the costs – usually is which device is the “best”. Characteristics where “more” or “less” is considered as “better” are seemingly easy to compare. This simplification, however, bears risks.
In digital photography, for instance, the size of the sensors and, thus, of the individual pixel in general, is more important than the total number of pixels. The pixel count however is commonly the relevant sales argument. For that reason, it makes sense to question the characteristics of a measuring device, as well as their definition and interaction. Often further information about the conditions under which these characteristics are valid such as temperature, position dependency etc, are missing.
Specifications usually contain the following characteristics: “measuring range”, “absolute accuracy” (also “correctness”), “repeatability” (also “precision”) and “measuring rate”.
“Measuring range” indicates minimum/maximum object sizes that are measurable. Sometimes, the visual range is specified instead, this means: the overall range in which the objects to be measured are allowed to move. Occasionally, information about the minimum and/or maximum measurable size is missing, too.
The colloquial meaning of “accuracy” is the total of all measuring errors. However, for the evaluation of a measuring device, it has to be differentiated: “absolute accuracy” means the comparison of a mean measuring value with a certified standard value.
“Repeatability” is defined as the scattering of the measuring values under the same conditions and, therefore, a characteristic of the measuring value noise of the device itself.
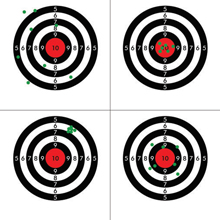
The sole specification of only a numerical value for “repeatability” is not sufficient. It might be that one supplier indicates the standard deviation of single values, whereas another calculates those based on a sequence of averaged values. A common visualisation of the definitions “absolute accuracy” (also called “correctness”) and “repeatability” (also called “precision”) is shown in Figure 1.
The “measurement rate” of a measuring device is the number of measurement values generated per second. This is a further important comparison criterion where “more” is seen as “better”. For an objective comparison, however, the knowledge of the interdependence between measurement rate and absolute accuracy and repeatability of a single measurement is crucial.
It may be the case that a measuring device with a higher measurement rate, but lower single value precision is less suitable for controlling or characterisation of a process than a device with a lower measuring rate but higher single value precision. For example, this is the case when a long averaging time is necessary due to a lower single value precision. Then, there is a risk that actual product variations, which occur within this averaging time, are levelled out while really present. In the worst case, the specifications might even be violated without being signaled by the measuring device.
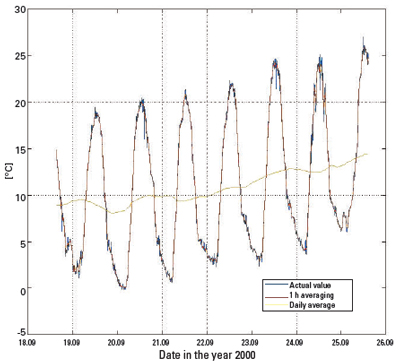
The following example of a temperature profile taken over a week in September 2000 shows to which extent averaging of a measuring value can influence the perception (Figure 2).
The displayed “real value” results from single measurements taken in 10-minute intervals. Averaging over a period of one hour only smoothens the extreme values. When averaging the varying temperature for more than 12 hours, the changes in temperature are displayed lower than they actually are.
Furthermore, if the mean value is generated over an entire day, the information about the daily temperature variations will be completely lost. A device that needs the latter averaging depth will not be suitable for a process where an alarm has to be raised or an adjustment has to be made depending on the temperature range.
A practical example taken from the hose and tube production process is the diameter measurement based on the shadow projection method with rotating mirrors. Often high measuring rates are indicated, which result from the rotation rate multiplied by the number of mirrors’ facets ([1] Zanoni, 1973; [2] Vossberg, 1981).

The specification of accuracy, however, is usually based on mean values of up to one second due to a relatively poor single value precision. This has various reasons. Each single measurement is done with a different mirror facet. Product movements during measurement increase or decrease the product diameter – depending on the direction of movement – as the measurement of both product edges is not done simultaneously but sequentially. Lastly, the diameter information is only derived from the very transition from dark to light and light to dark. The rest of the time, the information content of the measurement signal is zero.
In contrast
to this,
for other
measuring
techniques
such as the
diffraction
method
([3] Blohm,
 Sikora, &
Beining,
2005; [4]
Blohm &
Sikora, 2017),
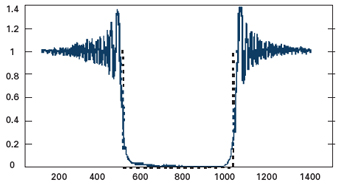
line scan
cameras are
used (figures
3 and 4).
Sikora, &
Beining,
2005; [4]
Blohm &
Sikora, 2017),
line scan
cameras are
used (figures
3 and 4).
On the one hand, product edges are recorded simultaneously – so product movement is not an issue. On the other hand, each single pixel in the diffraction seam outside the product shadow can be directly linked to the product edges. This leads to a much higher single value precision and consequently, the measuring value has to be averaged nowhere near as long to be used for controlling or characterisation of a production process.
Conclusion
A mere comparison of measuring rates without considering these circumstances is obviously not sufficient. Hence, for an objective comparison of two measuring devices, at first, it is important to clearly define the requirements of the process. Also, the catalogue details given by the manufacturer should be taken into question and brought to a comparable basis using the information needed, so that the investment in a new measuring device leads to an increase in quality, process optimisation as well as cost savings.
References:
[1] Zanoni, C. (1973). Patentnr. US3856412A. USA.
[2] Vossberg, C. A. (1981). Patentnr. US4269514A. USA.
[3] Blohm, W., Sikora, H., & Beining, A. (2005). Patentnr.
US6922254B2. USA.
[4] Blohm, W., & Sikora, H. (2017). Patentnr. US9797712B2.
USA.
Subscribe to Get the Latest Updates from PRA Please click here
©2018 Plastics and Rubber Asia. All rights reserved.

©2018 Plastics and Rubber Asia. All rights reserved.
Home Terms & Conditions Privacy Policy Webmail Site Map About Us

































































